Esta é a primeira de uma série de postagens sobre como montar os esteios de uma casa. Aqui, vou trazer um pouco da minha experiência e apresentar alguns conceitos de análise estrutural para podermos entender melhor como as peças de uma casa funcionam e como elas resistem às cargas aplicadas sobre elas. Na segunda postagem, discutirei duas opções de apoios para esteios, explicando alguns sub-casos, suas vantagens e desvantagem. Por fim, tentarei construir um resumo esquemático do que foi apresentado nas duas primeiras partes, com a esperança de que o caso do esteio sirva como exemplo para outras peças da construção.
Como escolher?
Qual é o melhor tipo de fundação para um esteio de madeira?
Depende!
Essa foi uma discussão recorrente quando eu morava em Maquiné. Toda vez que alguém aparecia com a vontade de construir uma casa, conversávamos sobre os prós e os contras, os guarani fazem assim, os colonos fazem assado, quanto duraria a madeira, vai usar cimento ou não, etc.
Como a própria pessoa iria construir sua casa, percebi dois aspectos não-técnicos se sobressaírem nessa avaliação do quê fazer:
- A herança cultural da pessoa: o ambiente em que havia crescido (geralmente urbano) somado ao seu pouco conhecimento sobre o funcionamento de estruturas trazia medos para o momento da decisão sobre como construir e o quê usar. Esses medos eram apaziguados pelas técnicas que ela estava mais familiarizada, ou seja, memórias vagas de construções vivenciadas.
- Usar o que está à mão: aqui entra, do lado romântico, a vontade de aproveitar o que a mãe natureza “oferece” (madeira do mato, barro, pedras, etc.), e, do lado prático, o pouco dinheiro disponibilizado para gastar numa aventura construtiva.
A galera que conheci que resolveu sair da cidade e ir para o mato estava sempre procurando conhecimento, devorando o que aparecia. Com razão, né? Tudo era novo. São generalistas incansáveis! Afinal, a pessoa, a partir do momento que está cuidando da sua água, comida, energia, etc., precisa saber um pouco de tudo mesmo. Obviamente, de construção também. Porém, sendo um generalista e autodidata há muitos anos, percebi uma desvantagem nessa postura: muita coisa fica só na superfície. Inventei um nome para isso: conhecimento de zine.
Os zines costumam ser pequenas cartilhas que apresentam um determinado tema e pode ser que ensinem a fazer algo prático também. Tu lês um zine e já sais querendo fazer acontecer. É ótimo! Mas pode criar aquela sensação prematura de “já sei como faz”. Na psicologia, isso é chamado de efeito Dunning-Kruger.

Além dos zines, outra fonte de conhecimento-superficial-que-gera-autoconfiança-sem-base-técnica é uma conversa com alguém mais experiente. A vizinha te conta super empolgada como foi que ela construiu sua casa e disso a gente rapidamente conclui que ali está um jeito bom de fazer (ainda mais se a casa estiver de pé). Claro que se a casa ainda está de pé, isso é um bom sinal. Mas quer dizer apenas que ela está de pé até agora.
E “estar de pé” não significa necessariamente durabilidade, boa climatização, facilidade de construção, baixo custo, construir com as próprias mãos, etc.
Bom, em termos de estrutura de uma casa, coloquei numa extremidade o conhecimento de zine. Na outra, vou colocar os cálculos estruturais: diagrama de corpo livre, tensor de tensões, momentos de inércia de cada elemento, etc. Ou seja, para cada forma e material, as contas vão dizer o que vai acontecer. Logo, te indicarão o que é melhor ser feito: onde reforçar e onde reduzir dimensões.
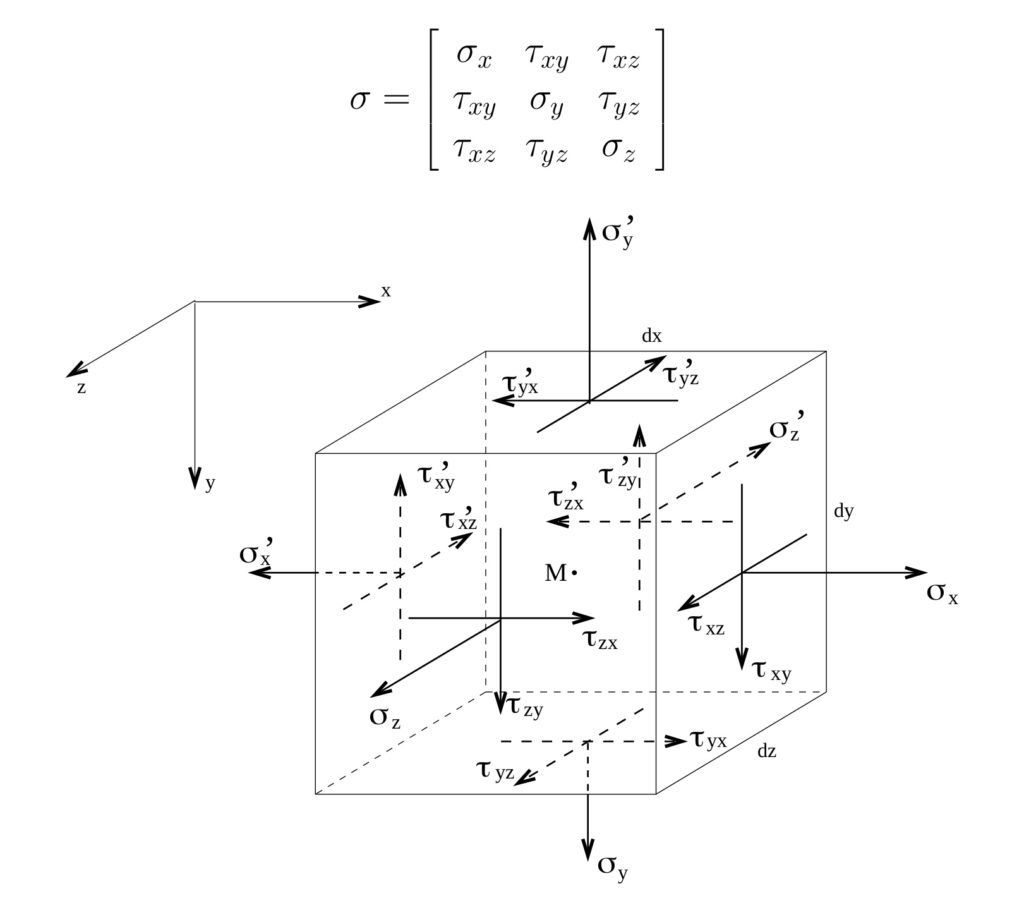
E a experiência prática vai enriquecer todo esse campo.
Faz muito tempo que estudei cálculo estrutural. Se me esforçar bastante, é provável que consiga reencontrar aquela habilidade. Mas acredito que ainda sobrou um pouco de conhecimento que virou intuição. Guardo comigo alguns princípios gerais do funcionamento dos materiais e soluções padrão de engenharia. Então, essa postagem será uma contribuição para o conhecimento de zine disponível, só que um pouco mais aprofundado.
Mostrarei agora algumas fotos de exemplos de fundações para termos ideia visual do que se trata essa conversa. Em seguida, virá um pouco de teoria.
Vejamos, então, os exemplos:










Um pouco de teoria: graus de liberdade
Tem um conceito da análise estrutural que se chama “graus de liberdade”. Imaginemos uma peça sozinha flutuando no espaço tridimensional (x-y-z). Se aplicarmos uma força na peça no sentido do eixo X (Fx), a peça irá se mexer ao longo do eixo X, pois não há resistência (ela está flutuando!). Se tentarmos girá-la em torno do eixo Y (Gy), ela irá girar naquele eixo. Para qualquer força aplicada, não há nenhuma restrição de movimento: ela pode ir pra frente e pra trás (Fx), pra cima e pra baixo (Fy) e prum lado e pro outro (Fz); além de poder girar em qualquer direção (Gx, Gy, Gz). Como são 3 eixos e 2 tipos de movimento para cada eixo (deslocamento e giro), uma peça flutuando no espaço possui, então, 6 graus de liberdade (movimentos possíveis).
Infelizmente, não consegui encontrar um vídeo que explicasse bem e com desenhos isso que descrevi no parágrafo anterior. Presencialmente com uma folha e uma caneta, acho que seria mais fácil.
A utilidade da propriedade graus de liberdade é podermos analisar que tipos de movimento uma determinada junção vai permitir (ou impedir) uma peça realizar. Poderia parecer óbvio que numa casa, num poste ou numa placa de sinalização que fica acima de e atravessa uma rodovia, tudo o que a gente quer é que a estrutura não se mexa de jeito nenhum (a junção chamada engaste tem zero grau de liberdade). Mas vejamos uma ponte ou de um trilho de trem. Ambos casos, a peça é de grande comprimento. Com as mudanças de temperatura, do dia e das estações do ano, ocorre a dilatação do material (o metal muda mais de tamanho que o concreto). Assim, temos que prever que a estrutura irá se mover, mas não devido à carga. Pelo menos, um dos apoios deve permitir movimento horizontal, como mostra a foto abaixo.

Treliças: tração ou compressão?
Outra situação contraintuitiva são as treliças. Não as de jardim, mas as que se usa para fazer pontes, torres de transmissão de energia e telhados. Quando uma peça está sofrendo flexão (ex. uma vara de pescar com um peixe na ponta ou uma árvore ao vento), de um lado da sua seção* o material está sendo comprimido, do outro, tracionado/puxado. Esse modelo é baseado na teoria da Linha Neutra: para cada forma, existe uma linha onde a tensão é zero, sendo que a tração cresce prum lado e a compressão para o outro. (* Numa tora, por exemplo, a seção transversal é a área redonda que aparece quando a gente corta-a transversalmente.)
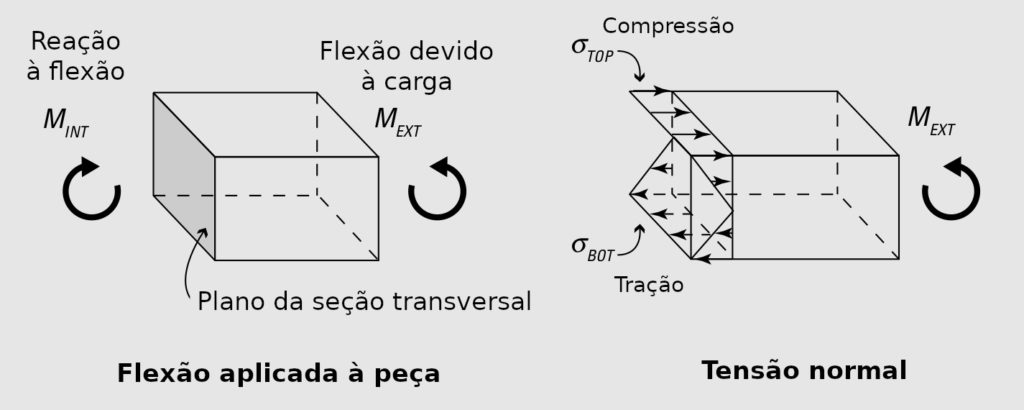
Bom, a galera descobriu que era possível distribuir melhor as tensões, além de reduzir o peso e o volume das peças, se elas estivessem sofrendo apenas tração ou compressão, e nada de flexão. Para isso, as junções entre as peças deveriam permitir o movimento de giro (um grau de liberdade). Ou seja, elas estariam unidas por uma rótula ou pivô. E deveriam ser formadas pela figura geométrica com menor número de lados: o triângulo. É isso que faz uma estrutura ser uma treliça: cada parte ou está sob tração, ou está sob compressão, e ser formada sempre por triângulos.

Então, as treliças são estruturas que se beneficiam de ter todas as junções permitindo um tipo de movimento, o giro em apenas um plano.
Esses são apenas dois exemplos em que não devemos usar o engaste (nenhum movimento possível). O apoio deve ser móvel para que tudo fique no lugar como planejado.
Formato dos perfis
Outra conclusão que se pode tirar dos cálculos usando a teoria da Linha Neutra é a seguinte: para cada tipo de carga (tração, compressão e/ou flexão) existe um perfil que irá suportá-la melhor. Os perfis otimizados pela engenharia mais comuns são os em formato de “I”, “L”, “T”, “U”, “H”.

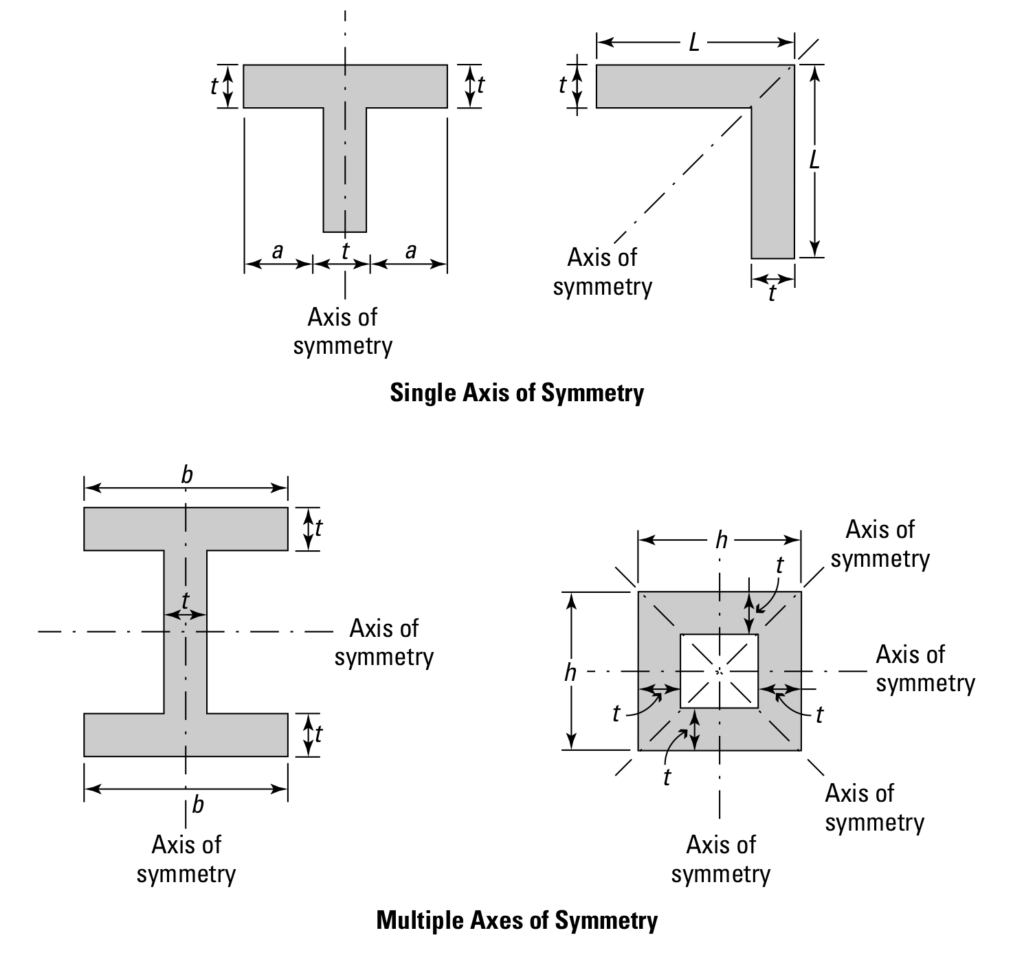
Por exemplo, os trilhos de trem são feitos com o perfil “I”. Várias estruturas de máquinas usam o perfil “U” ou “L”, assim como torres de transmissão de energia e galpões com estrutura metálica. Já os postes e suportes de placas de sinalização tem seção quadrada ou redonda, mas oca.
Claro que além da função estrutural, as peças precisam funcionar para o seu propósito e também ter boa cara. Mas por enquanto, estamos prestando atenção apenas para sua resistência.
O que gostaria de ressaltar aqui é que, diferente de uma peça maciça, os perfis listados acima são feitos de “vazios”. Um dos poucos exemplos que temos na natureza dessa economia de material é o bambu. Tanto uma tora quanto um bambu, ambos têm seção circular. Porém, se conseguirmos encontrar um bambu que resista à tração, por exemplo, o mesmo que uma tora, veremos que a peça de bambu pesará bem menos que a tora.
Na construção com madeira também aparece essa economia nos perfis. Por exemplo, por que é melhor usar caibros e não barrotes para a estrutura de um piso ou telhado? O perfil retangular na vertical aguenta muito mais que um perfil quadrado de mesma massa.


Dependendo da disponibilidade de materiais para sua construção e ferramentas, pode ser melhor cortar aquelas toras enormes e pesadas em dois caibros ou 4 barrotes e facilitar a sua vida (e prolongá-la tb!!).
Até onde consigo pensar, a única situação (olhando somente para o aspecto estrutural) que vale a pena usar uma tora inteira é quando a peça está majoritariamente sob compressão. E olhe lá!
Na próxima postagem, vou aplicar essa teoria para os esteios e suas possíveis fundações. Então, retomarei os exemplos reais para analisá-los e ver se podemos tirar alguns critérios para poder escolher melhor (ou pelo menos, saber as vantagens e as limitações da nossa escolha).
Referências:
- Mechanics of Materials for Dummies, James H. Allen III